1.3: Trigonometric Functions

• Gilbert Strang & Edwin “Jed” Herman
• OpenStax

Learning Objectives

• Convert angle measures between degrees and radians.
• Recognize the triangular and circular definitions of the basic trigonometric functions.
• Write the basic trigonometric identities.
• Identify the graphs and periods of the trigonometric functions.
• Describe the shift of a sine or cosine graph from the equation of the function.

Trigonometric functions are used to model many phenomena, including sound waves, vibrations of strings, alternating electrical current, and the motion of pendulums. In fact, almost any repetitive, or cyclical, motion can be modeled by some combination of trigonometric functions. In this section, we define the six basic trigonometric functions and look at some of the main identities involving these functions.

Radian Measure

To use trigonometric functions, we first must understand how to measure the angles. Although we can use both radians and degrees, radians are a more natural measurement because they are related directly to the unit circle, a circle with radius 1. The radian measure of an angle is defined as follows. Given an angle \(θ\), let \(s\) be the length of the corresponding arc on the unit circle (Figure \(\PageIndex\)). We say the angle corresponding to the arc of length 1 has radian measure 1.

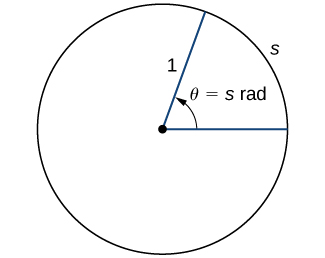From this point, there is one line segment that extends horizontally to the right a point on the edge of the circle and another line segment that extends diagonally upwards and to the right to another point on the edge of the circle. These line segments have a length of 1 unit. The curved segment on the edge of the circle that connects the two points at the end of the line segments is labeled “s”. Inside the circle, there is an arrow that points from the horizontal line segment to the diagonal line segment. This arrow has the label “theta = s radians”." width="325px" height="258px" />

Since an angle of \(360°\) corresponds to the circumference of a circle, or an arc of length \(2π\), we conclude that an angle with a degree measure of \(360°\) has a radian measure of \(2π\). Similarly, we see that \(180°\) is equivalent to \(\pi\) radians. Table \(\PageIndex\) shows the relationship between common degree and radian values.

Converting between Radians and Degrees

1. Express \(225°\) using radians.
2. Express \(5π/3\) rad using degrees.

Solution

Use the fact that \(180\) ° is equivalent to \(\pi\) radians as a conversion factor (Table \(\PageIndex\)):

1. \(225°=225°⋅\left(\dfrac\right)=\left(\dfrac\right)\) rad
2. \(\dfrac\) rad = \(\dfrac\)⋅\(\dfrac\)=\(300\)°